• Home

• Code

• Resources

• Teaching

• Talks

• People

• Contact

• CV

• Photography

• Music

Code

Please see the AMA code release at the BurgeLab GitHub repository for our most update-to-date code:

http://github.com/burgelab

Accuracy Maximization Analysis (AMA) - Matlab and C code implementation

Relevant publications: Please cite the following papers if the code on this page

or in the GitHub repository contributes to your research

• Burge J, Jaini P (2017). Accuracy Maximization Analysis for sensory-perceptual tasks: Computational

improvements, filter robustness, and coding advantages for scaled additive noise. PLoS Computational

Biology, 13(2): e1005281. doi:10.1371/journal.pcbi.1005281 [ pdf ]

• Jaini P, Burge J (2017). Linking normative models of natural tasks with descriptive models of neural

response. bioarXiv, doi:https://doi.org/10.1101/158741 [ pdf ]

• Burge J, Geisler WS (2015). Optimal speed estimation in natural image movies predicts human

performance. Nature Communications, 6: 7900, 1-11 doi:10.1038/ncomms8900 [ pdf ]

• Burge J, Geisler WS (2011). Optimal defocus estimation in individual natural images. Proceedings of

the National Academy of Sciences, 108 (40): 16849-16854 [ pdf ]

• Geisler WS, Najemnik J, Ing AD (2009). Optimal stimulus encoders for natural tasks. Journal of

Vision, 9(13):17, 1-16 [ pdf | correction ]

Download: AMAengine.zip ( more info: AMAengine_ReadMe.rtf )

Description: Computes the posterior probability of a category given the filter response(s) to the stimulus

Setup: (1) Download and unzip AMAengine.zip

(2) Put all five unzipped files in the current folder and/or in a folder on the Matlab path

(3) At the command prompt type: >> mex AMAengine.cpp

...OR, if it errors out, type: >> mex -compatibleArrayDims AMAengine.cpp

(4) At the command prompt type: >> help AMAengine

(5) At the command prompt type: >> AMAengineTest;

Use: AMA requires computing the posterior probability of each stimulus category given the filter responses

for every stimulus in the training set

To use AMA, a minimization routine and an objective function must be chosen

Note that the minimization routine and objective function are not fundamental to the AMA procedure

To get you started, an example minimization routine and an example objective function are provided

However, other minimization routines and/or objective functions may better suit your needs

The example below uses Matlab’s fmincon.m to find AMA filters that minimize the average relative

entropy of the posterior probability distributions over the categories, across all stimuli in the training set.

NOTE! Please download the code from github link above for the most recent and best functioning code. The code pasted

below is best thought of as very detailed pseudo code, rather than code that should be copied and used as is.

Troubleshooting (Matlab R2011a, R2011b, R2012a and Xcode 4.2, Xcode 4.3)

Any combination of these versions of Mathworks & Apple software may prevent Matlab from finding the C++ header files

To fix the issue, go to http://www.mathworks.com/support/solutions/en/data/1-FR6LXJ/ and follow the instructions

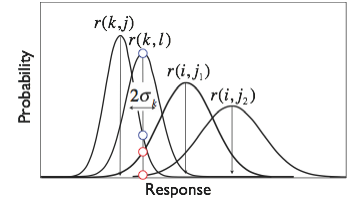
(1) Select stimulus: s(k,l)

(2) Noisy response due to that s(k,l): N(r(k,l),sigma(k,l))

(3) Noisy responses due to other stims in same Ctg: N(r(k,j),sigma(k,j))

(4) Noisy responses due to other stims in other Ctgs: N(r(i,j),sigma(i,j))

(5) Likelihood of response r(k,l) from s(k,l)

(6) Likelihood of response r(k,l) from s(k,j) and s(i,j)

(7) Posterior probability of correct category X(k) given s(k,l)

(8) Repeat for all other stimuli in the training set

Logic:

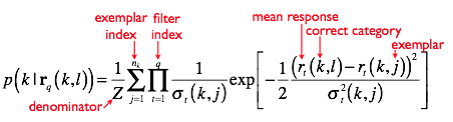
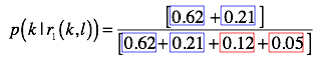
All code is published under the GNU General Public License: this software is free; you can

redistribute it and/or modify it under the terms of the GNU General Public License (GPLv3)

Please report bugs to jburge@mail.cps.utexas.edu with subject jburge.cps.utexas.edu/Code

%%% OBJECTIVE FUNCTION %%%

function C = objFunc(f,s,ctgInd,X,cstType,rMax,fano,v0)

% function C = objFunc(f,s,ctgInd,X,cstType,rMax,fano,v0)

% objective function for AMA

% f: filters. vector magnitude of each filter must equal 1 [ nDim x nF ]

% s: stimuli. vector magnitude of each stimulus must equal 1 [ nStm x nDim ]

% ctgInd: category indices of each stimulus (must be integer valued) [ nStm x 1 ]

% NOTE! number of unique values in ctgInd number of levels in X

% X: latent variable values [ 1 x nLvl ]

% cstType: cost type [ 1 x nLvl ]

% rMax: max mean response (i.e. if cos similarity btwn f and s = 1.0 [ scalar ]

% fano: fano factor... how neural noise variance scales w mean response [ scalar ]

% v0

% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% C: average cost to minimize [ 1 x 1 ]

% INPUT HANDLING

if min(ctgInd) == 0, error(['objFunc: WARNING! min(ctgInd) must be equal 1']); end; % error check

% MEAN FILTER RESPONSE(S) TO ALL STIMULI

r = stim2resp(f,s,rMax);

% STDDEV OF FILTER RESPONSE(S) TO ALL STIMULI

sigma = resp2sigma(r,fano,v0);

% POSTERIOR PROB AT CORRECT CTG (pp [nStm x 1]) & ALL CTGs (ppAll [nStm x nLvl]) FOR ALL STIMULI

[pp,ppAll] = AMAengine(r,r,sigma,ctgInd);

% NUMBER OF STIMS

nStm = size(s,1);

% NUMBER OF STIMS

if strcmp(cstType,'KLD')

% AVERAGE COST ACROSS STIMULI (KL DIVERGENCE BTWN IDEALIZED & ACTUAL POSTERIOR PROBABILITY DSTBs)

Call = -log2(pp); % average relative entropy in bits

elseif strcmp(cstType,'L0N')

% AVERAGE COST ACROSS STIMULI

Call = 1 - pp; % posterior map is optimal for L0 norm cost function

elseif strcmp(cstType,'L2N')

% POSTERIOR MEAN (optimal estimate for L2norm cost function)

Xhat = sum(bsxfun(@times,ppAll,X),2);

% COST FOR EACH STIMULUS

Call = ((Xhat - X(ctgInd)').^2);

end

% AVERAGE COST ACROSS STIMULI

C = sum(Call,1)./nStm;

%%% MINIMIZATION ROUTINE %%%

>> [f] = fmincon(@(f) objFunc(f,s,ctgInd,X,cstType,rMax,fano,v0),f0,[],[],[],[],[],[],@(f) fConEq(f));

%%% CONSTRAINT FUNCTION %%%

function [c,ceq] = fConEq(f)

c = [];

ceq = sum(f.^2,1)-1; % vector magnitude of filters must equal 1.0

%%% RESPONSE FUNCTION %%%

function [r] = stim2resp(f,s,rMax)

r = rMax.*(s*f); % mean filter response [ nStm x nF ]

%%% SIGMA FUNCTION %%%

function [sigma] = resp2sigma(r,fano,v0)

sigma = sqrt( fano.*abs(r) + v0 ); % stddev of filter response [ nStm x nF ]